
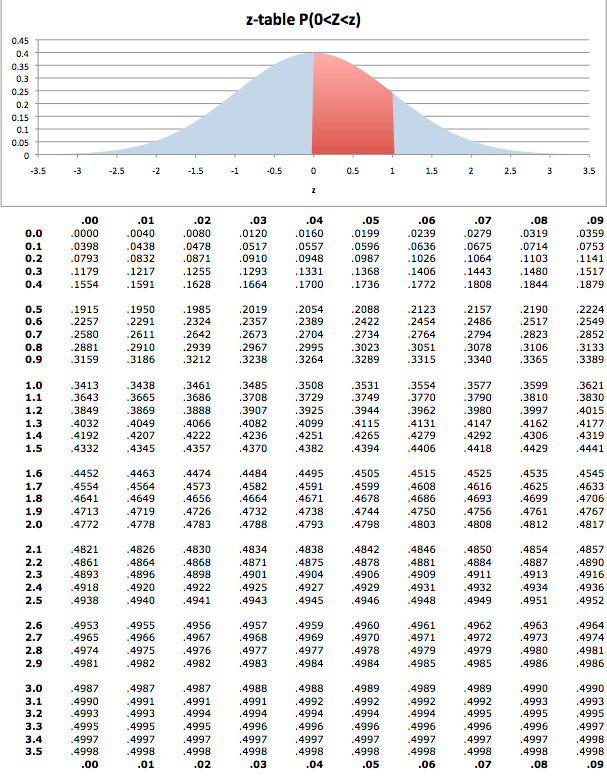
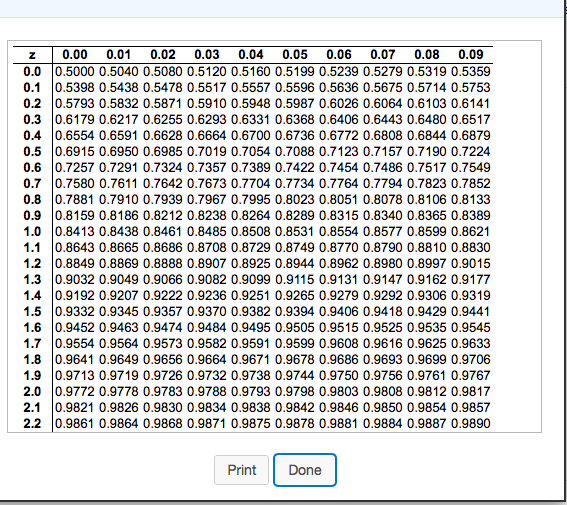
Since the z-score is negative, look for the value -1.5 in the negative z-table: 0.06681 (or 6.681%).Compute the z-score: 𝑧 = (64 - 70) / 4 = -1.5 (this result means that a score of 64 points is 1.5 standard deviations below the mean).Since the z-score is positive, look for the value 1.25 in the positive z-table: 0.89435 (89.435% of the students scored less than 75 points).įollowing the previous example (𝜇 = 70 and 𝜎 = 4), what proportion of students scored more than 64 points?.Compute the z-score: 𝑧 = (75 - 70) / 4 = 1.25 (this result means that a score of 75 points is 1.25 standard deviations above from the mean).What is the z-score of the value 75? In other words, what proportion of students scored less than 75 points? Suppose the scores on a college exam are normally distributed with a mean 𝜇 of 70 and a standard deviation 𝜎 of 4. The intersection between the column and the row corresponds to the p-value.Look at the topmost row of the table and find the column that matches the second part of your z-score (e.g.Look at the leftmost column of the table and find the row that matches the first part of your z-score (e.g.
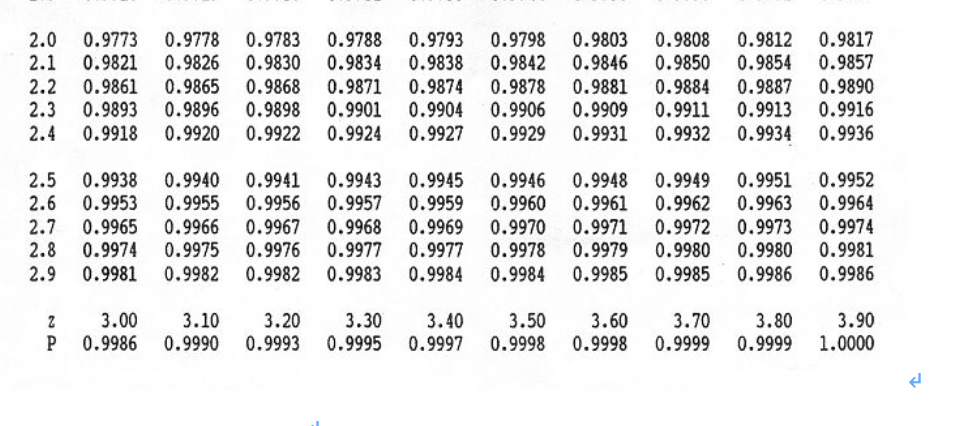
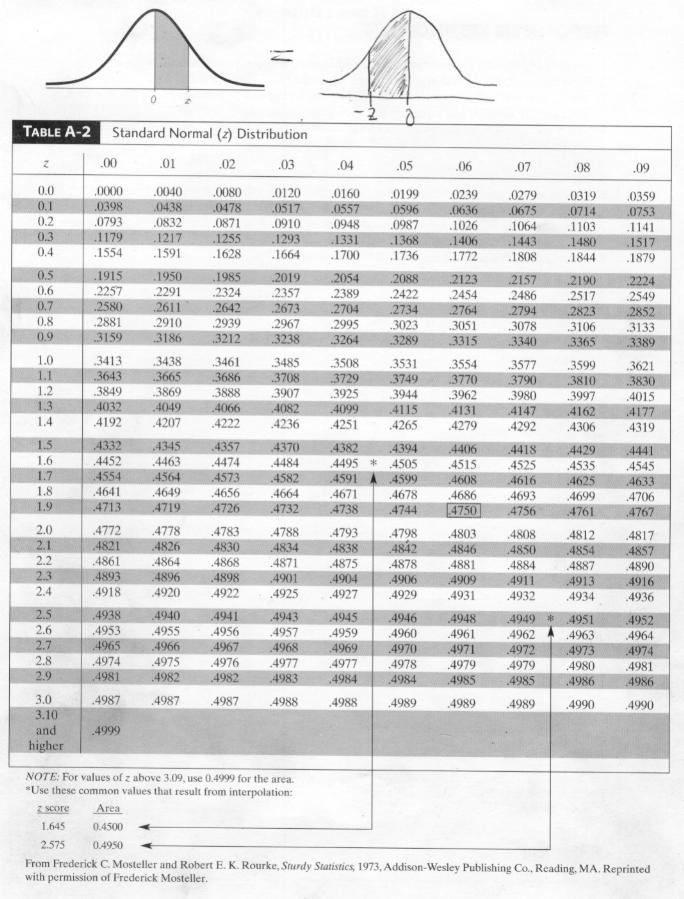
The second part is made up of the remaining digit (i.e. The first part goes up to the first digit after the decimal (i.e. If it's positive, use a positive z-score table. If it's negative, use a negative z-score table. A z-score is basically a standardized variable that has been rescaled to have a mean µ of 0 and a standard deviation σ of 1 (which ultimately provides a standard set of z-values - from the z-table - that can be used for easy calculations). It is calculated with the following formula: 𝑧 = (𝑋 − 𝜇) ⁄ 𝜎 (where 𝑋 is the data point, 𝜇 is the population mean, and 𝜎 is the population standard deviation). A z-table, also called standard normal table, is a table used to find the percentage of values below a given z-score in a standard normal distribution.Ī z-score, also known as standard score, indicates how many standard deviations away a data point is above (or below) the mean.Ī positive z-score implies that the data point is above the mean, while a negative z-score indicates that the data point falls below the mean.


 0 kommentar(er)
0 kommentar(er)
